Gerbo Technology - Tesseract

to English Version

Tesseract

De tesseract is een vier dimensionale hyperkubus. Wat is een hyperkubus? Wat is de vierde dimensie? Hoe ziet een vier dimensionaal object eruit?

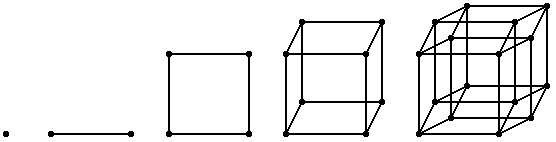
Om de vierde dimensie beter te kunnen begrijpen, gaan we eerst kijken naar eenvoudigere dimensies. Voor nul dimensies hebben we een punt. Voor de eerste dimensie trekken we het punt opzij om een lijn te maken. Voor de tweede dimensie trekken we de lijn omhoog en krijgen zo een vierkant. En voor de derde dimensie trekken we het vierkant naar achteren om een kubus te krijgen. Nu de vierde dimensie. We trekken de kubus "ana" or "kata", de twee richtingen in de vierde dimensie, om zo een a tesseract te krijgen. Als we willen, kunnen we op deze manier doorgaan voor hyperkubussen van hogere dimensies. De onderstaande tabel toont de progressieve toename van onderdelen.

dimensies	onderdelen	0	1	2	3	4	5
hoofd object		punten	lijnen	vierkanten	kubussen	tesseracten	5D hyperkubussen
0	punt	1	-	-	-	-	-
1	lijn	2	1	-	-	-	-
2	vierkant	4	4	1	-	-	-
3	kubus	8	12	6	1	-	-
4	tesseract	16	32	24	8	1	-
5	5D hyperkubus	32	80	80	40	10	1

Links

Op het web is veel materiaal te vinden over de vierde dimensie, hyperkubussen en in het bijzonder de tesseract. Ken Perlin en Harry J. Smith tonen prachtige roteerbare draadframes van de tesseract. En vergeet ook niet de Tesseract Schermbeveiliging.