Gerbo Technology - Tesseract

naar de nederlandse versie

Tesseract

The tesseract is a four dimensional hypercube. What is a hypercube? What is the fourth dimension? What does a four dimensional object look like?

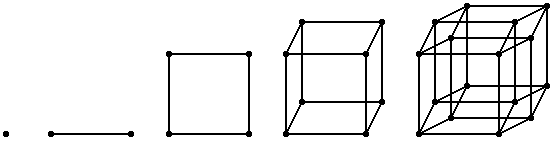
To help us better understand the fourth dimension, we will first look at the simpler dimensions. For zero dimensions, we will have a point. For the first dimension, we will drag the point sideways to make a line. For the second dimension, we will drag the line upwards to get a square. And for the third dimension, we will drag the square backwards to get a cube. Now for the fourth dimension. We will drag the cube "ana" or "kata", the two fourth dimension directions, to get a tesseract. If we wanted to, we could go on this way to get higher dimensional hypercubes. The table below shows the progressive increase of parts.

dimensions	parts	0	1	2	3	4	5
main object		points	lines	squares	cubes	tesseracts	5D hypercubes
0	point	1	-	-	-	-	-
1	line	2	1	-	-	-	-
2	square	4	4	1	-	-	-
3	cube	8	12	6	1	-	-
4	tesseract	16	32	24	8	1	-
5	5D hypercube	32	80	80	40	10	1

Links

On the web a lot of work can be found about the fourth dimension, hypercubes and the tesseract in particular. Ken Perlin and also Harry J. Smith present beautiful rotateble wireframes of the tesseract. And don't forget the Tesseract Screen Saver.